‘Aggregate Demand, Idle Time, and Unemployment’ – A Critique of Michaillat and Saez
Introduction
Like all neoclassical models, that of Michaillat and Saez (2014) referred to in Simon Wren-Lewis’s Mainly Macro blog on 16th August fails to model money realistically. This renders their model incoherent and in any case incapable of encompassing one of the most important causes of unemployment: inadequate aggregate demand due to monetary factors.
The chief feature of their model is a product market in which matching is the mode of exchange. This produces costly frictions that lead output to apparently run ahead of consumption. To make sense of demand that does not automatically follow from income Michaillat and Saez introduce a ‘non-produced good’ which is endowed to every household. When households meet to exchange goods there is mutual trade of this non-produced good and households’ individually produced goods so as to optimise each household’s joint holding in utility terms. Michaillat and Saez ascribe a relative price p to the production good, which apparently becomes the absolute price when they determine the price of the non-produced good as 1. Since it is determined in equilibrium it is important that p is an absolute price, otherwise quantities of exchanges, production and labour demanded would be indeterminate in the model as they would also depend on the rate of exchange between the produced and non-produced goods. In fact it turns out that claiming p to be an absolute price is untenable.
Relative and Absolute Prices
When one trader meets another trader and they agree to exchange different goods, eg: apples and pears, the ratio in which they are exchanged gives us ‘relative prices’. If they agree to exchange every 10 apples from the apple-grower for 8 pears from the pear-grower then the relative price of apples to pears is 10/8 or 1.25 and the relative price of pears to apples is 8/10 or 0.8. To convert these relative prices to absolute prices we need to nominate one the fruits as a ‘numeraire’ and normalise its price to 1. If we choose apples then the absolute price of a pear is 0.8; if pears then the price of an apple is 1.25. For all other goods that can be exchanged directly with either good an absolute price can be established.
Prices in the Model
The difficulty with Michaillat and Saez’s model is that their trades do not involve one good being directly traded for another but bundles of two goods, the non-produced and the produced good, in different quantities. This is summarised in their household budget constraint:
![]()
where m is the quantity of nonproduced goods purchased at price 1; µ the quantity of nonproduced goods sold at price 1; f(x).k, the quantity of produced goods sold at price p and c the quantity of produced goods purchased at price (1+tau(x)).p. To find the implied relative price for the produced good we need to solve this budget constraint for p, which yields
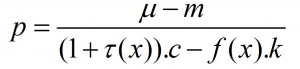
To determine this relative price we need to know the quantities of both goods changing hands in the transaction, ie: the difference in nonproduced and the difference in produced goods held before and after trading. To convert this relative price to an absolute price we then need to nominate one of these differences as a numeraire. Crucially, this difference cannot be identified until after trading has taken place, and so the numeraire can play no part in trading decisions and no absolute price can be adjusted to (or determine) equilibrium. The authors’ claim to have set the value of a non-produced good itself as the numeraire is thus incoherent.
To make this scenario more concrete let us imagine that the endowed good is water. Every household has a supply of water, but either the amount they have varies, households’ utility from a given quantity of water varies, or both. When households meet in exchange they rebalance their bundles of goods by mutual exchange of water and produced goods. The ratio of water and produced goods exchanged will vary according to initial water endowments, production functions, and utility functions for water and produced goods. For each household the utility value to them of the combination of water and produced goods received must equal that of those given up, but there are multiple bundles of the two goods that can achieve any particular utility value and so the absolute values of the goods involved in each exchange are indeterminate. As a result fixing a numerical price value on either of the two goods (as opposed to the difference in goods) cannot convert a relative price into an absolute price in this model.
Money in a Modern Economy
The important implication is that what Michaillat and Saez have constructed is a model of a barter economy, not a monetary one. Essentially, the specific problem of matching frictions that they identify could be regarded as a negative good for which the barter or production of other goods must be made to overcome. Say’s law thus holds and so equilibrium and employment are determined by supply factors alone, including the supply of product-market friction-busting.
In contrast, a true monetary model of the economy must involve a ‘non-produced’ good which obtains its value from the giving up of goods and services that provide utility. In this way only can the non-produced good be used as a numeraire and be an alternative ‘purchase’ to real goods and services. But what could fulfil this role? The best answer is the credible promise of a future flow of real goods and services, in the form of a token of a credit agreement. A recent article in the Bank of England Quarterly Bulletin has, rather belatedly to many of us, described the creation of money in a modern economy in precisely these terms (McLeay et al. 2014).
As soon as the existence of a continuous flow of circulating credit tokens (in the form of coin, banknotes, or bank deposits) into and out of the economy is recognised, combined with the intrinsic uncertainty of a complex social structure, a radically different explanation for fluctuations in employment becomes apparent. Credit and money creation is itself subject to expectations, and so also is the desire to hold money rather than to spend it in exchange for immediate consumption or investment. Low levels of money creation and the holding rather than spending of money will reduce demand for goods and labour, whether or not matching frictions exist, and are almost certainly more significant causes of socially-damaging unemployment.
References
Michaillat, P. and Saez, E. (2014) ‘Aggregate Demand, Idle Time, and Unemployment’ Working Paper 18826, National Bureau of Economic Research, revised July 2014.
McLeay, M., Radia, A. and Thomas R. (2014) ‘Money Creation in the Modern Economy’ Bank of England Quarterly Bulletin Q1, pp1-14.